2.3. Exercices#

2.3.1. Calcul du nombre de chemins#

Dans cet exercice, nous allons compter le nombre de chemin possible entre deux points d’un quadrillage. Nous considérons donc un quadrillage, chacun des points aura deux coordonnées entières (l’absisse et l’ordonnée). Le point de départ est pour simplifier le point \((0,0)\).

L’objectif est de déterminer le nombre de chemins possibles permettant d’atteindre le point \((i, j)\) en respectant la règle suivante : seuls les déplacements vers la droite (\(i\) croissant) et vers le haut (\(j\) croissant) sont autorisés.

La figure suivante représente deux chemins possibles pour relier le point \((0,0)\) au point \((4, 3)\).

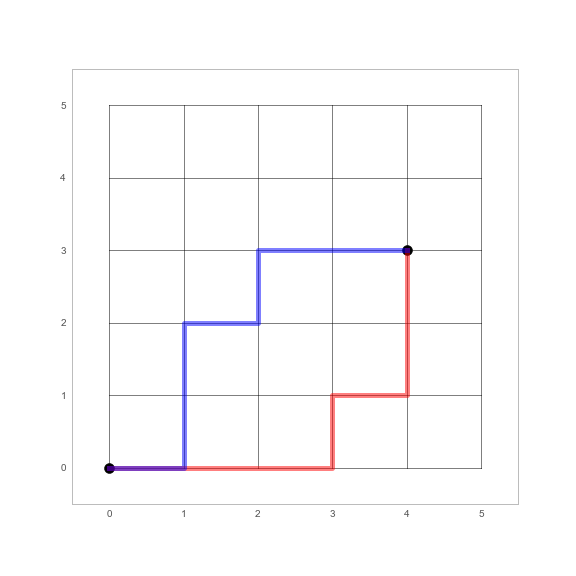
exemple

Indication

Pour atteindre le point \((i, j)\), il faut nécessairement passer soit par le point \((i-1,j)\) soit par le point \((i, j-1)\) et ces deux types de chemins sont obligatoirement différents. Par ailleurs, si \(i=0\) ou \(j=0\), il n’y a qu’un seul chemin possible.

En notant \(N_{i, j}\) le nombre de chemins pour relier le point \((0,0)\) au point \((i, j)\), on a donc les relations suivantes

\[\begin{split} N_{i, j} = \left\lbrace \begin{aligned} &1, &\text{si } i=0 \text{ ou } j=0,\\ &N_{i-1, j} + N_{i, j-1}, &\text{si } i>0 \text{ et } j>0. \end{aligned} \right. \end{split}\]

Question

L’objectif est d’afficher le nombre de chemins possibles pour aller au point de coordonnées \((3, 4)\).

  • Construisez une liste de listes notée nb_chemins telle que nb_chemins[i][j] soit égal à \(0\). Essayez d’utiliser la compréhension de listes.

  • Remplissez la liste nb_chemins pour que nb_chemins[i][j] soit égal au nombre de chemins pour aller en \((i, j)\).

  • Affichez proprement le nombre de chemins pour aller en \((3, 4)\).

Hide code cell source 
i, j = 3, 4
nb_chemins = [[0 for l in range(j+1)] for k in range(i+1)]
for k in range(i+1):
    for l in range(j+1):
        if k == 0 and l == 0:
            nb_chemins[k][l] = 1
        if l > 0:
            nb_chemins[k][l] += nb_chemins[k][l-1]
        if k > 0:
            nb_chemins[k][l] += nb_chemins[k-1][l]
print(f"Le nombre de chemins pour aller en ({i}, {j}) vaut {nb_chemins[i][j]}")

Le nombre de chemins pour aller en (3, 4) vaut 35

Question

Nous allons à présent afficher les différents chemins.

  • Modifiez le script précédent pour que la liste contienne une liste des chemins possibles plutôt que le nombre de chemins. Vous appelerez cette liste liste_chemins. Un chemin sera une liste de tuples contenant les coordonnées des points parcourus.

  • Affichez les 35 chemins qui mènent au point de coordonnées \((3, 4)\).

Hide code cell source 
i, j = 3, 4
liste_chemins = [[[] for l in range(j+1)] for k in range(i+1)]
for k in range(i+1):
    for l in range(j+1):
        if k == 0 and l == 0:
            liste_chemins[k][l] = [[(0, 0)]]
        if l > 0:
            lkl = []
            for lv in liste_chemins[k][l-1]:
                lkl.append(lv + [(k, l)])
            liste_chemins[k][l] += lkl
        if k > 0:
            lkl = []
            for lv in liste_chemins[k-1][l]:
                lkl.append(lv + [(k, l)])
            liste_chemins[k][l] += lkl

print(f"Les chemins pour aller en ({i}, {j}) sont ")
for l in liste_chemins[i][j]:
    print(l)
print(f"Il y a {len(liste_chemins[i][j])} chemins possibles")

Les chemins pour aller en (3, 4) sont 
[(0, 0), (1, 0), (2, 0), (3, 0), (3, 1), (3, 2), (3, 3), (3, 4)]
[(0, 0), (1, 0), (2, 0), (2, 1), (3, 1), (3, 2), (3, 3), (3, 4)]
[(0, 0), (1, 0), (1, 1), (2, 1), (3, 1), (3, 2), (3, 3), (3, 4)]
[(0, 0), (0, 1), (1, 1), (2, 1), (3, 1), (3, 2), (3, 3), (3, 4)]
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (3, 2), (3, 3), (3, 4)]
[(0, 0), (1, 0), (1, 1), (2, 1), (2, 2), (3, 2), (3, 3), (3, 4)]
[(0, 0), (0, 1), (1, 1), (2, 1), (2, 2), (3, 2), (3, 3), (3, 4)]
[(0, 0), (1, 0), (1, 1), (1, 2), (2, 2), (3, 2), (3, 3), (3, 4)]
[(0, 0), (0, 1), (1, 1), (1, 2), (2, 2), (3, 2), (3, 3), (3, 4)]
[(0, 0), (0, 1), (0, 2), (1, 2), (2, 2), (3, 2), (3, 3), (3, 4)]
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (2, 3), (3, 3), (3, 4)]
[(0, 0), (1, 0), (1, 1), (2, 1), (2, 2), (2, 3), (3, 3), (3, 4)]
[(0, 0), (0, 1), (1, 1), (2, 1), (2, 2), (2, 3), (3, 3), (3, 4)]
[(0, 0), (1, 0), (1, 1), (1, 2), (2, 2), (2, 3), (3, 3), (3, 4)]
[(0, 0), (0, 1), (1, 1), (1, 2), (2, 2), (2, 3), (3, 3), (3, 4)]
[(0, 0), (0, 1), (0, 2), (1, 2), (2, 2), (2, 3), (3, 3), (3, 4)]
[(0, 0), (1, 0), (1, 1), (1, 2), (1, 3), (2, 3), (3, 3), (3, 4)]
[(0, 0), (0, 1), (1, 1), (1, 2), (1, 3), (2, 3), (3, 3), (3, 4)]
[(0, 0), (0, 1), (0, 2), (1, 2), (1, 3), (2, 3), (3, 3), (3, 4)]
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 3), (2, 3), (3, 3), (3, 4)]
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4)]
[(0, 0), (1, 0), (1, 1), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4)]
[(0, 0), (0, 1), (1, 1), (2, 1), (2, 2), (2, 3), (2, 4), (3, 4)]
[(0, 0), (1, 0), (1, 1), (1, 2), (2, 2), (2, 3), (2, 4), (3, 4)]
[(0, 0), (0, 1), (1, 1), (1, 2), (2, 2), (2, 3), (2, 4), (3, 4)]
[(0, 0), (0, 1), (0, 2), (1, 2), (2, 2), (2, 3), (2, 4), (3, 4)]
[(0, 0), (1, 0), (1, 1), (1, 2), (1, 3), (2, 3), (2, 4), (3, 4)]
[(0, 0), (0, 1), (1, 1), (1, 2), (1, 3), (2, 3), (2, 4), (3, 4)]
[(0, 0), (0, 1), (0, 2), (1, 2), (1, 3), (2, 3), (2, 4), (3, 4)]
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 3), (2, 3), (2, 4), (3, 4)]
[(0, 0), (1, 0), (1, 1), (1, 2), (1, 3), (1, 4), (2, 4), (3, 4)]
[(0, 0), (0, 1), (1, 1), (1, 2), (1, 3), (1, 4), (2, 4), (3, 4)]
[(0, 0), (0, 1), (0, 2), (1, 2), (1, 3), (1, 4), (2, 4), (3, 4)]
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 3), (1, 4), (2, 4), (3, 4)]
[(0, 0), (0, 1), (0, 2), (0, 3), (0, 4), (1, 4), (2, 4), (3, 4)]
Il y a 35 chemins possibles

2.3.2. Nombre de possibilités#

Nous allons alculer le nombre de possibilités pour faire 1 euro avec des pièces de \(1\), \(2\), \(5\), \(10\), \(20\), \(50\) centimes. Il n’est pas nécessaire d’afficher les possibilités.

Question

Programmez une méthode naïve consistant à imbriquer des boucles les unes dans les autres.

Nous remarquons qu’il est possible de décomposer l’algorithme de la manière suivante :

  • créez une liste ways contenant des 0 de taille 101 (\(101=1+100\) où 100 centimes = 1 euro). L’élément \(i\) de cette liste est destiné à contenir le nombre de possibilité de faire \(i\) centimes avec le jeu de pièces.

  • On remarque ensuite que si on a que des pièces de 1 centime,

    • le nombre de possibilité pour faire 1 centime est 1 ;

    • le nombre de possibilité pour faire \(i\) centimes est \(0 + 1 = 1\).

  • On ajoute ensuite les pièces de 2 centimes. Pour faire une somme de \(i\geq2\) centimes, il y a deux types de solution : soit sans pièces de 2 centimes (c’est le nombre déjà calculé ways[i]) ou bien avec au moins 1 pièce de 2 centimes (c’est le nombre ways[i-c]). Donc ways[i] = ways[i] + ways[i-c].

  • On ajoute ensuite toutes les pièces 1 par 1 pour calcules les possibilités.

Question

Programmez la méthode efficace ci-dessus.

Hide code cell source 
target = 100*10
coinSizes = [1, 2, 5, 10, 20, 50, 100, 200]
ways = 0
S0 = target
for i0 in range(S0//coinSizes[7]+1):
    S1 = S0 - i0*coinSizes[7]
    for i1 in range(S1//coinSizes[6]+1):
        S2 = S1 - i1*coinSizes[6]
        for i3 in range(S2//coinSizes[5]+1):
            S3 = S2 - i3*coinSizes[5]
            for i4 in range(S3//coinSizes[4]+1):
                S4 = S3 - i4*coinSizes[4]
                for i5 in range(S4//coinSizes[3]+1):
                    S5 = S4 - i5*coinSizes[3]
                    for i6 in range(S5//coinSizes[2]+1):
                        S6 = S5 - i6*coinSizes[2]
                        #for i7 in range(S6//coinSizes[1]+1):
                        #    ways += 1
                        ways += S6//coinSizes[1] + 1
                    
print(f"Il y a {ways} façons de faire {target} avec des pièces de {coinSizes}")

Il y a 321335886 façons de faire 1000 avec des pièces de [1, 2, 5, 10, 20, 50, 100, 200]
Hide code cell source 
target = 100*10
coinSizes = [1, 2, 5, 10, 20, 50, 100, 200]
ways = [0] * (target + 1)
ways[0] = 1
for c in coinSizes:
    for i in range(c, target+1):
        ways[i] += ways[i-c]
print(f"Il y a {ways[-1]} façons de faire {target} avec des pièces de {coinSizes}")

Il y a 321335886 façons de faire 1000 avec des pièces de [1, 2, 5, 10, 20, 50, 100, 200]