Large topological entropy implies
existence of a maximal entropy measure for interval maps
Discrete
Contin. Dyn. Syst. Ser. A, 14 (4), 673-688, 2006.
Abstract
We give a new type of sufficient condition for the existence of
measures with maximal entropy for an interval map f, using
some non-uniform hyperbolicity to compensate for a lack of smoothness
of f. More precisely, if the topological entropy of a
C1 interval map is greater than the sum of the
local entropy and the entropy of the critical points, then there
exists at least one measure with maximal entropy. As a corollary, we
obtain that any C r interval map f such that
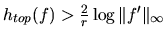 possesses measures with maximal entropy.
possesses measures with maximal entropy.
Paper:
[arXiv:1901.01073]
[pdf (published paper)]