Dense chaos for continuous interval maps
Nonlinearity,
18, 1691-1698, 2005.
Abstract
A continuous map f from a compact interval I into itself is
densely chaotic if the set of points (x,y) such that
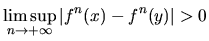 and
and
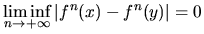 is dense in I 2.
We show that if f is a densely chaotic interval map then
f 2 has
a horseshoe, which implies that its topological entropy is at least
log 2/2 and f is of type at most 6 for Sharkovskii's order
(that is, there exists a periodic point of period 6).
is dense in I 2.
We show that if f is a densely chaotic interval map then
f 2 has
a horseshoe, which implies that its topological entropy is at least
log 2/2 and f is of type at most 6 for Sharkovskii's order
(that is, there exists a periodic point of period 6).
Paper:
[arXiv:1901.01064]
[pdf (published paper)]