 Bertrand Maury
Bertrand Maury

Equipe
ANEDP,
Laboratoire de
mathématiques, Université Paris-Sud
Professeur associé au DMA,
Ecole Normale Supérieure.
Membre du bureau d'AMIES
Bureau 2A5, bâtiment 307
Laboratoire de Mathématiques, Université Paris Sud
91405 Orsay Cedex
01 69 15 74 91
Bertrand.Maury @ math.u-psud.fr
Publications
Research interests
Particulate
flows
Fluid-particle solvers
Handling of contacts
(dry and lubricated)
Modeling
of the respiratory system
Modelling
of crowd motions
Optimization
under constraint
Particulate
flows
Direct simulation of fluid particle flows
To simulate the motion of rigid particles in a viscous fluid, we firstly
used the so-called Arbitrary
Lagrangian Eulerian approach, which relies on an unstructured mesh
that follows the motion of the particles (see [6],
1999)). This method relies on an unstructured mesh which locally fits the
boundary of the particles (click on the mesh to see an animation of a moving
periodic mesh in the case of sedimentating particles):
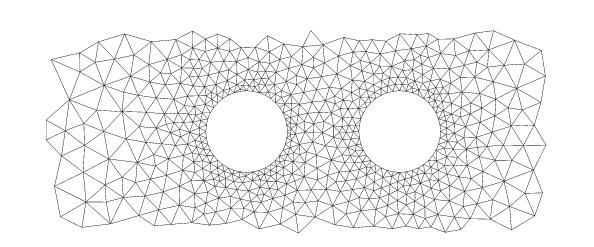
The mesh moves smoothly as the time goes on, until its quality gets too low,
making it necessary to rebuild a new mesh, onto which the current velocity
field is to be projected. We developped a Finite Element code, which handles
biperiodic boundary conditions. This code is currently used by Julien
Couder, at IPGP, to model sedimentation flows. It is thoroughly described in
[6]. Note that contacts are handled in this
approach by a very rough method, which cannot be properly justified
from the modelling standpoint, but which makes computations quite robust.
See below some remarks on
better (or, at least, more justified) ways to handle those contacts.
With a former PhD student, Mourad
Ismail, we proposed and developped a completely different approach to
handle rigid particles in a fluid domain, namely the Fat
Boundary Method. In the spirit of the Fictitious Domain Method, as
developped by Roland Glowinski
, this method makes it possible to use a cartesian mesh, on which fast
solvers can be used. Yet, the way to take the particles into account is
quite different, as it is based on a domain decomposition approach with
overlapping: the domain is decomposed onto a large (fictitious) domain which
covers the mixture, and a set of narrow domains surrounding the particles.
See [9] for a presentation of this method for
the Poisson problem, and [14] or Mourad
Ismail's homepage for applications to Navier-Stokes flows. It has not
been implemented with high order Finite Element, but theoretical
analysis (joint work with Silvia Bertoluzza, see [14])
suggests an optimal convergence rate, which is not common for FE
approximation on a mesh which does not respect the boundary of the domain.
In order to provide a simple tool to compute fluid-particle flows, we (with
Joāo Janela and Aline
Lefebvre, a student at Orsay) applied the penalty
method to this type of problem. The rigid body motion is simply
obtained by forcing the strain to be small within the bodies (penalty
method). This approach is similar to what is done by Caltagirone's team in
Bordeaux. Compared to the previous method, it presents the drawback to
change the operator which acts on the velocity: it destroys the
well-ordered hierachical spectral structure of the Laplace operator, and
consequently rules out the possibility to use standard fast solver for the
global system. On the other hand, this method is quite easy to implement (it
can be done in a few lines with the free software Freefem++
). An application of this method to a simple model of (rigid) cardiac valve
is presented in [18] (2005).
Note that, for particulate flows, contacts still need to be handled in a
proper way. To that purpose, Aline
Lefebvre adapted the method proposed in [20], and a
FreeFem++ script to simulate fluid-particle flows in a robust way is now
available. More complex constraints can be easily added to the
numerical model, e.g. particles which are subject to remain at a given
distance.
Despite its conceptual simplicity, error estimates in both h and epsilon
(the penalty parameter) are not straightforward to obtain for this method.
We established the expected error in h^(1/2) + epsilon for a scalar
version of the rigid motion constraint [29].
Blood flows
The techniques presented previously to simulate the motion of rigid
particles in a fluid can be applied to study the equivalent viscosity of
complex mixtures like blood. As a first step, we can consider that red blood
cell are rigid, and surrounded by a newtonian fluid (the non-newtonian
character of the blood at a larger scale is precisely due to the presence of
red cells). We performed some computations of collection of rigid bodies in
a fluid submitted to a shear motion. See [22]
(2005) for some computations (based on the ALE approach) of the effective
viscosity of a mixture of a viscous fluid and interacting, rigid bodies.
With S. Martin, S. Faure, and T. Takahashi, we are currently working on more
realistic representations of the actual red blood cells. Each cell is
modelled as an assembly of 11 spheres, submitted to spting-like
interaction forces to mimic their deformability. Click on the picture
below to download an avi movie (37 Mo) representing those cells aggregating
under the action of some interaction forces.

Contacts
/ granular flows
Initially motivated by the need to handle numerical collisions in the
direct simulation of fluid particle flows, we developped a code to compute
the motion of (2D or 3D) spherical grains, under the assumption of
non-elastic shocks. Moving obstacles can be taken into account, as the
following animations illustrate.
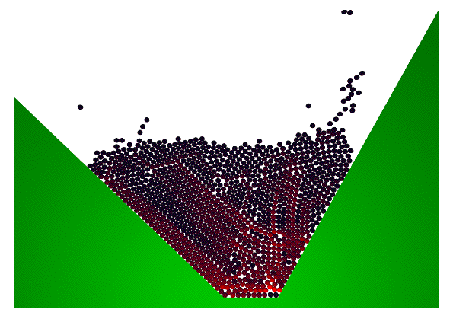



This method is presented and analysed in [20]
(2006). It is unconditionnaly stable (large time steps can be used), and can
be shown to convergence in the case of a single contact. Note that this
convergence is up to a subsequence, as the solution to the evolution
equation is not unique, even if the data is regular (only analyticity
ensures uniqueness, as showed by M.
Schatzman). The scheme we propose is able to recover 2 different
solutions associated to the same set of data, as detailed in [20]
(two subequences of time steps converge to two different solution to the
very same problem). This is somewhat anecdotical from the modelling
standpoint, as the forcing term which leads to non-uniqueness is not likely
to be faced in nature, but this situation is rare enough to be
mentioned.
For wet grains, interaction (lubrication) forces between neighbouring
particles can be taken into account.
It motivated the approach presented in [4], which
is based on an asymptotic expansion of the normal and tangential interaction
forces between two spheres in relative motion. This method leads to
badly conditionned matrices, which are difficult to handle numerically. We
recently proposed an simplified version of this lubrication model (see [25],
2007). This model has been extended to many-body situations by A.
Lefebvre.
This model is somewhat paradoxal: whereas it is designed to handle
interaction between rigid bodies in a highly viscous fluid (so that
lubrication force play a significant role before actual contact, because of
surface roughness for example, occurs), it is obtained as the vanishing
viscosity limit of a lubrication model. This apparent contradiction is
discussed in [25] (2007), and more thoroughly
in Aline
Lefebvre's PhD thesis.
Coagulation fragmentation
We applied granular flow techniques to the simulation of coagulation
phenomena. The coagulation is obtained by turning on an strong attractive
force when two particles get into contact. The method is detailed in [16] (2004).
Animations to download (1.1 Mb, 1.9 Mb, and 3.9 Mb)



Note that, if computations can be carried out with no harm, this
second-order evolution problem with unilateral constraints and stochastic
forcing term does not fit into any standard class of problems. Following a
discussion we had last december, Jean
Bertoin established the first theoretical results concerning this type
of problem, in the case of a single contact (see link).
Crowd motion
A simple model for crowd motion can be build up in the spirit of
granular flow models with non-elastic shocks. With Juliette
Venel, a PhD student at Orsay, we are working on the theoretical
aspects of this model, and proposed a numerical scheme to discretize it.
This work is ongoing. See an example of 1000 persons evacuating a square
room with obstacles in front of the exit
(.gif, 2.9 Mb), or, for those who are
familiar with the RER station Gare du Nord, another example (gif,
6Mb). This model takes the form of a differential inclusion,
with a difficulty due to the non convexity of the feasible set: the
multivalued operator is not maximal monotone. It is indeed the outward
normal cone to a set which is not convex (set of discs with non-overlapping
constraint). But as the set is prox-regular, recent results by L.
Thibault provide a sound theoretical framework for this model, see [24],
a poster
realized for the CANUM 2006, or [38].
More recently
Free
surface flows
This activity dates back to the PhD I did at University Paris 6, under the
supervision of O. Pironneau, on the flat glass forming process. I
developped a 3D Navier-Stokes Finite Element solver for free surface
flows with surface tension. We introduced a new method to advect a free
surface, which may be called projected characteristics, as an advection
equation is solved on a plane around each point of the surface by a method
of characteristics. This method allows to use large time steps (no CFL
condition is required). It is presented in detail in [2].
Another issue was raised by the surface tension forces, which are
proportionnal to the mean curvature. We show (see [2]
again) that this curvature can be integrated in the standard variational
setting. We established the convergence (order 1/2 in h, the mesh diameter)
of this way to take into account the surface tension for a 2D problem (see [23]).
See below a stationary state for a 2D model of the float glass forming
process (the molten glass floats over a bath of tin).
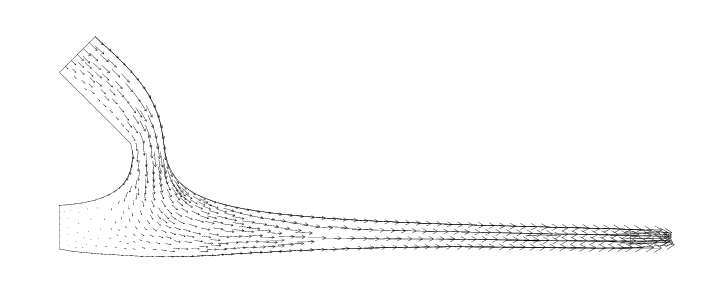
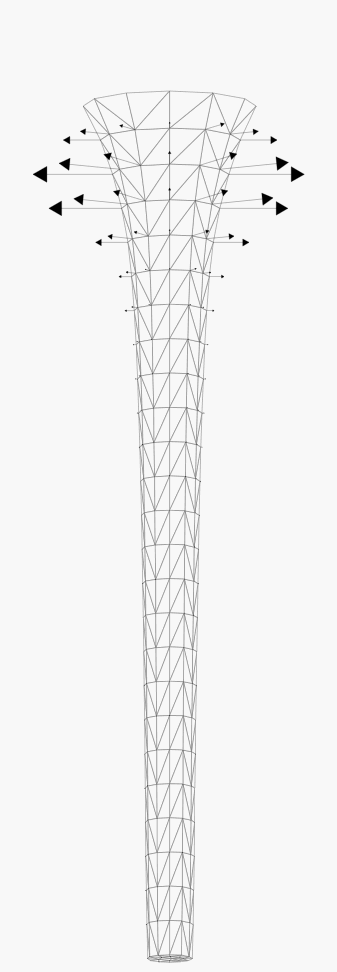
The next set illustrate the stability of the characteristic method to advect
the free surface, in case of a surface velocity with a predominating
tangential component (about 4 time steps between each snapshot).
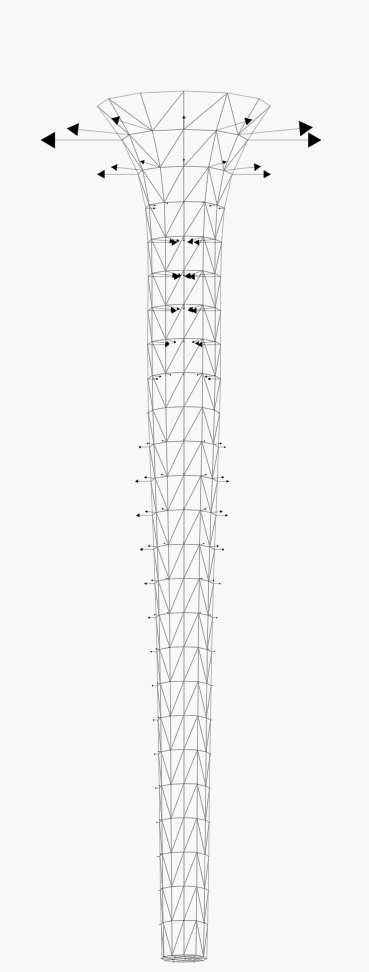
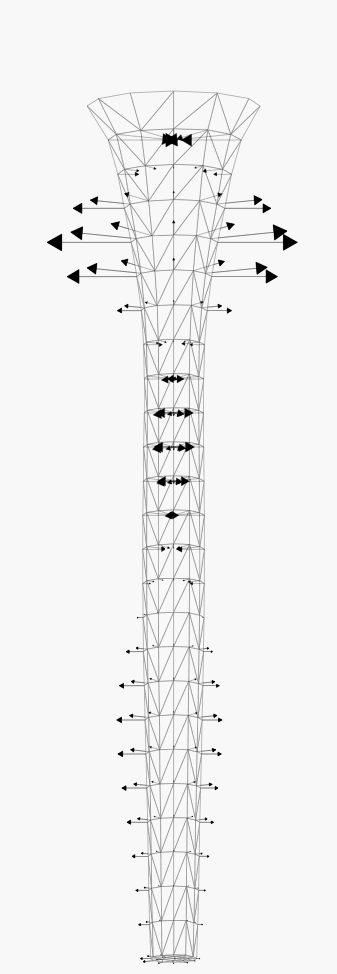
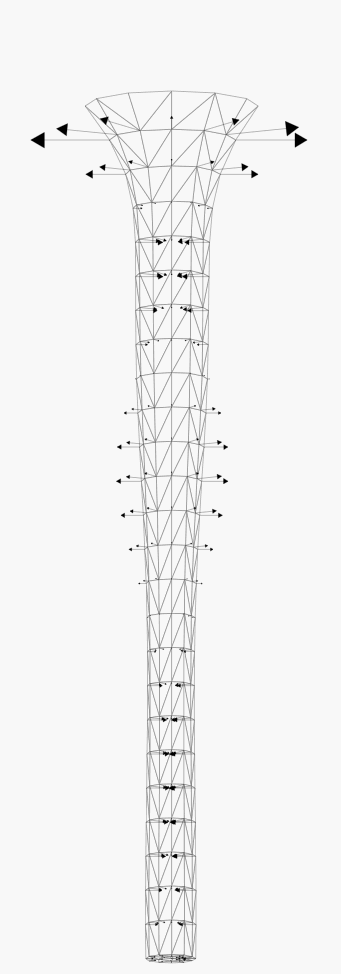
Modelling
of the respiratory system
This activity started within the Project
ACINIM LePoumonVousDisJe.
Our activities concentrated on the following aspects :
- design of suitable outlet boundary
condition at interfaces between the upper part of the tree (where
the flow obeys Navier-Stokes equations) and the distal part (where the air
flow flows Stokes equations, and therefore can be described by means of
Poiseuille-type laws). We proposed BC which we called dissipative, as they
involve the equivalent Poiseuille relation in the downstream subtree, and
lead to dissipative term in the variational formulation. Different forms of
those conditions are described in [19] (2005).
Three-dimensional experiments were performed (collaboration with C.
Grandmont and L.
Baffico).
- coupling of the Navier-Stokes part to a spring-mass system to model the
paremchyma:
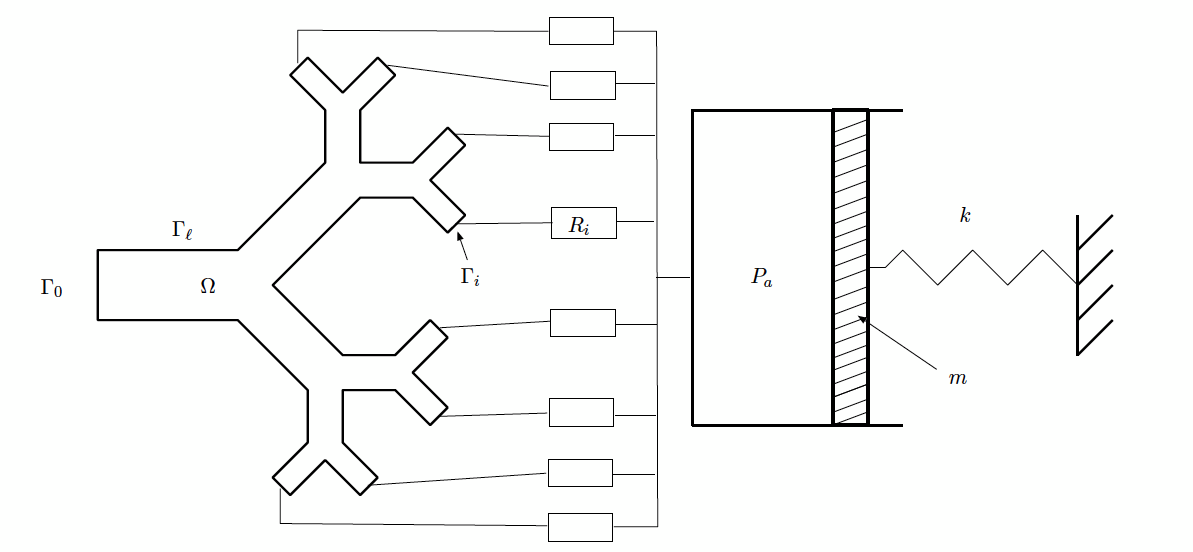
With this approach, the ventilation is caused by a force acting on the
piston (which represents the paremchyma). This model was first introduced in
[17] (2005). A theoretical analysis of
this model and some numerical test are proposed in [26]
(2007).
- Investigation of the role of the smooth
muscle in the ventilation process. This is a joint work
with Sebastien Martin
(Orsay), Thomas Similowski, and Christian Strauss (Pitié-Salpêtrière,
Paris). We proposed a simple respiration model process
(ventilation + diffusion of O2 in the blood) to investigate the (possibly)
positive role of smooth muscle contraction upon the overall efficiency of
the respiratory process. This work has been publisshed in [29].
- Coupling of a bronchial tree (assuming Poiseuille law is verified
for all branches) with a spring mass system (1D model for the paremchyma).
With C.
Grandmond and N. Meunier (see [21], 2006), we
obtained a new constitutive equation (in the one-dimensional case) for
an elastic media perforated with holes containing an incompressible gas,
which communicate through a network of pipes through which the gas flows and
dissipates energy. It leads to a wave-like equation with a non local
dissipative term. It is not clear whether the damping is exponential or not.
This very point is presently investigated by C. Grandmont and C. Vannier.
- Elaboration of an infinite tree
model to describe in some way the regularity of the pressure field within
the paremchyma. This work, somewhat exploratory and, for the time
being, academic, addresses the following question : the pressures at
alveolae form a set of discrete values (1 value per alveola, about 300
million in the human lung), uniformly distributed over the space domain
occupied by the paremchyma. It is tempting to replace this collection of
values by a continuum.
As a first step (with C. Vannier, PhD student) we had the number of
generations of the actual tree (23 in practice) "go to infinity". We
obtain an infinite dyadic, resistive tree T, on which a Sobolev space H^1
can be defined (set of nodal pressures which dissipate a finite rate of
energy). The question is now whether a trace space can be defined (the
boundary of T can be identified with the space of random
walks in Z). We obtain a non trivial trace space (H^1/H^1_0 is not {0}) as
soon as the global resistance if finite (which is the case for the infinite
version of a healthy lung). The next step (in collaboration with Delphine
Salort) consists in imbedding the infinite set of leaves (=alveolae in
practice) onto a real domain in R^d, in order to investigate the possibility
to identify natural functional spaces for the pressure, and describe the
regularity of feasible pressure fields. Under suitable assumptions (regular
tree, regular embedding of the set of ends in the domain) we establish that
the pressure field presents some sort of regularity in space: it
belongs to H^0.15 (for d = 3).
This work is described in [30].
Unclassified
Optimization under constraint
With Guillaume Carlier and Thomas Lachand-Robert, we considered the
problem which consists in projecting
a function onto the cone of convex
functions for the H1 norm. This problem is quite flat
from a theoretical point of view, yet finding an effective way to
approximate the solution to this problem is much less straightforward.
One of the difficulties is that the piecewise P1 interpolation of a convex
function is itself not convex in general, which rules out the possibility to
handle the convexity constraint in a standard, strong way (the constrained
discretized space is "too small").
A first answer to that problem was proposed by Thomas Lachand-Robert. it
consists in working on the larger space of all those piecewise P1 functions
which are not necessarily convex, but which interpolate a convex function.
This relaxed constraint at the discrete level can be expressed in terms of
values of the discrete function at the nodes of the triangulation. Note that
most of those constraints are non local. With Guillaume Carlier, we analysed
and implemented this method (see [10], 2001). A
convergence result can be established for this method, but it is still too
expensive to be applied to real life problems.
Therefore we followed a completely different strategy, which relies on a
dual expression of the convexity constraint. Numerical computations
(presented in [7]) exhibits a fairly
satisfactory behaviour, yet the numerical analysis of the approach is
difficult because the continuous saddle-point formulation is ill posed. The
problem takes the following abstract form: Let Ac by the cone of convex
functions (in H1(O)). Let B be a Hilbert space (in our case
the set of L2 function defined over O times O ). Ac is identified
with the reciprocal range by C of a convexe cone Bo+
in B, which is defined as the polar cone to B+, closed convex
cone of B (in our case the set of nonnegative functions, onto which it is
easy to project, which is what the method relies on). Now the problem is:
the range of C is not closed, so that neither uniqueness nor existence for
the Lagrange multiplier is guaranteed. There are infinitely many ways
to bluid up C, for the convexity constraints, but none of them (at least
among those we have considered) has the closed range property. Those
considerations are detailed in [7] (1999).
Full analysis of the method has not been done, but the
fairly good behaviour of the algorithm can be explained by the following
consideration: in the continuous version of the Uzawa algorithm (seen as a
time-discretization of a gradient flow in the space of Lagrange
multipliers), we established weak convergence (at least of a subsequence) of
the primal trajectory to the solution to the minimization problem, even in
the case the saddle-point problem is ill-posed (i.e. the Lagrange multiplier
does not exist). The proof is given in [12]
(2003), and it suggests at least why the parameter in the Uzawa algorithm
does not degenerate as h (the mesh diameter) goes to 0.
Note that all this is related to the general study of the asymptotic
behaviour of the solution to an homogeneous differential inclusion
involving a maximal monotone operator, which has been intensively studied in
the 70's. Yet, to our knowledge, none of the standard results include
the case of a maximal monotone operator whose range does not contain 0
(which is the problem we face here).
Maximization of the first
eigenvalue of the Laplace operator with respect to the domain
With Geoffroy Billotey, student at Ecole Polytechnique, we developped
a numerical tool, to investigate the following problem: Given N circles with
same radius r, in a bounded domain, find the configuration which maximizes
the smallest eigenvalue of the Laplacian with Dirichlet boundary conditions.
After some elementary spectral analysis of the heat equation, this problem
can be expressed from a modelling point of view: given a hot plate and a set
of coolers, where to put them in order to optimize the cooling process? This
work is not published.
The method is simply based on a gradient flow associated to the
smallest eigenvalue seen as a functional of the center locations.
The following animation represents the trajectory of ten particles, which
converges toward a (local ?) maximum of the first eigenvalue (Download
2.4 Mb, .avi). This second animation corresponds to the same situation
with a different initial conditions; it converges, after a short nap around
a seemingly quasi-equilibrium point, to a situation symmetric to
the previous one (Download 5.7 Mb, .avi).
Publications
[73] J.-L. Cercos-Pita, L. Fardin, H. Leclerc, B. Maury, G. Perchiazzi, A. Bravin, S. Bayat,
Lung Tissue Biomechanics Imaged with Synchrotron Phase Contrast Microtomography in Live Rats,
Scientific Reports - Nature volume 12, Article number: 5056 (2022),
Download
[72] F. Al Reda, B. Maury, Game-Theoretic and Inhibition-Based models for crowd motion ,
Comptes Rendus. Mathématique, Tome 359 (2021) no. 9, pp. 1071-1083., HAL.
[71] F. Bourdin, B. Maury, Multibody and macroscopic impact laws: a
Convex Analysis standpoint (2020), HAL.
[70] H. Lavenant, B. Maury, Opinion
propagation on social networks : a mathematical standpoint,
ESAIM: Proceedings and Surveys, 2020, Vol. 67, p. 285-335, ESAIM
Procs, HAL
[69] A. Decoene, S. Martin, B. Maury, Direct simulation of rigid
particles in a viscoelastic fluid, in Journal of Non-Newtonian Fluid 260
(october 2018) HAL.
[68] B. Maury, S. Faure, J.
Angelé, R. Bachimont, A Time -continuous Compartement Model for Building
Evacuation, Third European Symposium on Fire Safety, Journal of Physics:
Conference Series, Volume 1107, Evacuation (link).
[67] B. Maury,
S. Faure, Crowds
in Equations,
London: World Scientific Publishing Europe Ltd, 2018, link
[66] B.
Grec, B. Maury, N. Meunier, and L. Navoret, A
1D model of leukocyte adhesion coupling bond dynamics with blood velocity,
J
Theor Biol. 2018
Mar 20;452:35-46. HAL.
[65] B Maury, Grains de foules, Gazette des Mathématiciens No 152, avril
2017 HAL.
[64] M. Fabre, S. Faure, M. Laurière, B. Maury, C. Perrin, Non classical
solution of a conservation law arising in vehicular trafic, ESAIM:
Proceedings and Surveys 55, 131-147, HAL.
[63] B. Maury, Congested
transport at microscopic and macroscopic scales
7th European Congress of
Mathematics (7ECM), Jul 2016, Berlin,
7ECM Proceedings, 2017 HAL.
[62] H. Guénard, J.-B. Martinot, S. Martin, B. Maury, S. Lalande, C.
Kays, In vivo estimates of NO and CO conductance for haemoglobin and forlung
transfer in humans, Respiratory Physiology & Neurobiology 228 (2016)
1–8.
[61] F. Al Reda, B. Maury, Interpretation of Finite Volume discretization
schemes for the Fokker Planck equation as gradient flows for the discrete
Wasserstein distance, Topological
Optimization and Optimal Transport: In the Applied Sciences 15, 333
HAL
[60] S. Di Marino, B. Maury, F. Santambrogio, Measure sweeping processes,
Journal of Convex Analysis, Special Volume dedicated to the memory of Jean
Jacques Moreau, 1923 - 2014, Vol. 23, Nr 2 (2016) HAL
[59] B. Maury, A. Preux, Pressureless Euler equations with maximal density
constraint : a time-splitting scheme, Topological
Optimization and Optimal Transport: In the Applied Sciences 17, 333
HAL
[58] S. Martin & B. Maury, Notion de résistance de l’arbre pulmonaire
bronchique dans la ventilation respiratoire humaine, in “Modéliser
& simuler”, Tome 2, Matériologiques, 2014.
[57] B. Maury, The resistance of the respiratory system, from top to bottom,
Esaim Proceedings and Survey, december 2014, Vol. 47, p. 75-96 pdf
[56] S. Faure, B. Maury, Crowd motion from the granular standpoint,
Mathematical Models and Methods in Applied Sciences Vol. 25, No. 3 (2015)
463–493 pdf.
[55] B. Maury, non smooth
evolution models in crowd dynamics: mathematical and numerical issues, in
Collective Dynamics from Bacteria to Crowds, An Excursion Through Modeling,
Analysis and Simulation, Series: CISM International Centre for Mechanical
Sciences, Vol. 553 (2014). pdf
[54] B. Maury, A. Roudneff-Chupin, F. Santambrogio, Congestion
driven dendritic growth, Discrete and Continuous Dynamical Systems, Volume
34, number 4, April 2014, preprint.
[53] B. Fabrèges, B. Maury, Approximation of Single Layer Distributions by
Dirac Masses in Finite Element Computations, Journal of Scientific
Computing, January 2014, Volume 58, Issue 1, pp 25-40 (arXiv).
[52] B. Fabrèges, L. Gouarin, B. Maury, A smooth extension method,
Comptes Rendus Mathematique, Volume 351, Issue 9, Pages 361-366 (2013)
pdf
[51] B. Maury, The Respiratory System in Equations (MS&A), ed.
Springer (book), 2013, link
[50] S. Martin, B. Maury, Modeling of the oxygen transfer in the respiratory
process,
ESAIM: Mathematical Modelling and Numerical Analysis / Volume 47 / Issue 04
/ July 2013, pp 935-960,HAL
.
[49] A. Decoene, B. Maury, Moving meshes with freefem++. Journal
of Numerical Mathematics. Volume 20, Issue 3-4, pp. 195–214 (2012).
[48] J. Dambrine, B. Maury, N. Meunier, A. Roudneff-Chupin, A
congestion model for cell migration, Communications on Pure and Applied
Analysis 11, 1 (2012) 243-260. (arXiv)
[47] Aline Lefebvre-Lepot, Bertrand Maury,
Numerical Modeling of Fluid-Grain Interactions, Close Interaction of
Immersed Grains, chapters 11 and 12 in Discrete Numerical Modeling of
Ganular Materials, arang Radjai, Frederic Dubois Eds., ISTE Ltd and John
Wiley & Sons Inc, march 2011 link.
[46] B. Maury, Prise en compte de la congestion dans les modèles de
mouvements de foules, in Actes des Colloques Caen 2012-Rouen 2011, pdf.
[45] Aline Lefebvre-Lepot, Bertrand Maury, Micro-Macro Modelling
of an Array of Spheres Interacting Through Lubrication Forces, Adv.
Math. Sci. Appl. 21 (2011), no. 2, 535–557, hal
[44] C. Grandmont, B. Maury, Integrated Multi-Model Description of the
Human Lungs, in Coupled Fluid Flow in Energy, Biology and Environmental
Research, E-Book Series Progress in Computational Physics (PiCP),
Volume 2, Matthias Ehrhardt (ed.), Bentham Science Publishers, Springer
2011. pdf
[43] A. Decoene, S. Martin, B. Maury, Microscopic modelling of active
bacterial suspensions,
Mathematical Modelling of Natural Phenomena 2011 6 (05) : pp 98-129 (hal).
[42] A. Decoene, A. Lorz, S. Martin, B. Maury, M. Tang, Simulation of
self-propelled chemotactic bacteria in a Stokes flow, ESAIM: Proceedings,
30, 105-124 (2010). (.pdf)
[41] B. Maury, A. Roudneff-Chupin, F. Santambrogio, J. Venel,
Handling Congestion in Crowd Motion Modeling, Networks and
Heterogeneous Media, Volume 6, Number 3, September 2011, pp. 485–519 (arxiv).
[40] F. Bernicot, B. Maury, D. Salort, A 2-adic approach of the
human respiratory tree, Netw. Heterog. Media 5 (2010), no. 3, 405–422
(arxiv).
[39] S. Bertoluzza , M. Ismail, B. Maury, Analysis of the fully
discrete Fat Boundary Method, Numerische Mathematik, Volume 118, Number 1,
49-77 (2011).
[38] B. Maury, J. Venel, A discrete Contact Model for
crowd Motion, ESAIM: M2AN 45 1 (2011) 145-168. (hal).
.
[37] C. Bui, P. Frey and B. Maury, A coupling strategy based on anisotropic
mesh adaptation for solving two-fluid flows, International Journal for
Numerical Methods in Fluids, Volume 66, Issue 10, August 2011, Pages:
1226–1247 (pdf).
[36] B. Maury, A. Roudneff-Chupin, F. Santambrogio, A macroscopic
Crowd Motion Model of the gradient-flow type, Mathematical Models and
Methods in Applied Sciences Vol. 20, No. 10 (2010) 1787-1821 (arxiv).
[35] A. Devys, C. Grandmont, B. Grec, B. Maury and D.Yakoubi, Numerical
method for the 2D simulation of the respiration, ESAIM: Proc., August 2009,
Vol. 28, p. 162-181 (link).
[34] S. Faure, S. Martin, B. Maury and T. Takahashi, Towards the simulation
of dense suspensions: a numerical tool, ESAIM: Proc., 2009, Vol. 28, pp.
55-79 (.pdf).
[33] L. Baffico, C. Grandmont, B. Maury, Multiscale Modelling of the
Respiratory Tract, Math. Models Methods Appl. Sci. 20 (2010), no. 1, 59-93 (.pdf).
[32] B. Maury, D. Salort, C. Vannier, Trace theorems for trees,
application to the human lung, Network and Heterogeneous Media, Volume 4,
Number 3, September 2009 pp. 469--500 (.pdf).
[31] B. Maury, J. Venel, A Mathematical Framework for a Crowd Motion Model,
C. R. Acad. Sci. Paris, Ser. I 346 (2008) 1245--1250.
[30] B. Maury, Numerical Analysis of a Finite Element / Volume Penalty
Method, SIAM J. Numer. Anal. Volume 47, Issue 2, pp. 1126-1148 (2009). (.pdf)
[29] S. Martin, T. Similowski , C. Strauss, B.
Maury, Impact of respiratory mechanics model parameter on gas exchange
efficiency, ESAIM Proc, June 2008, Vol. 23, p. 30-47 (link).
[28] V. Girault, H. Lopez, B. Maury, Energy balance of a 2-D model for
lubricated oil transportation in a pipe, Divulgaciones Matematicas Vol. 16
No. 1(2008), pp. 87--105 (pdf).
[27bis] S. Del Pino, B. Maury, 2d/3d turbine simulations with freefem++, in
Numerical Analysis and Scientific Computing for PDEs and their Challenging
Applications, J. Haataja, R. Stenberg, P. Raback and P. Neitaanmäki, eds,
CIMNE, Barcelona, Spain, 2008. (.pdf
1Mo)
[27] C. Bui, P. Frey, B. Maury, Methode du second membre modifié
pour la gestion de rapports de viscosité importants dans le probleme de
Stokes bifluide, C. R. Mecanique 336 (2008) 524--529.
[26] C. Grandmont, B. Maury, A. Soualah, Multiscale
modelling of the respiratory track : a theoretical framework (2007),
Proc, June 2008, Vol. 23, p. 10-29 (.pdf).
[25] B. Maury, A gluey particle model, ESAIM Proceedings,
July 2007, Vol.18, 133-142
Jean-Frédéric Gerbeau & Stéphane Labbé, Editors (.pdf,
200
kb).
[24] B. Maury, J. Venel, Un modèle de mouvements de foule
(in french), ESAIM Proceedings, July 2007, Vol.18, 143-152,
Jean-Frédéric Gerbeau & Stéphane Labbé, Editors (.pdf,
964
kb).
[23] V. Girault, H. Lopez, B. Maury, One time-step finite
element discretization of the equation of motion of two-fluid flows,
Numerical Methods for Differential Equations, vol. 22. 3, pp. 680-707, 2006
(.pdf, 200 kb).
[22] A. Lefebvre, B. Maury, Apparent viscosity of a
mixture of a Newtonian fluid and interacting particles, Fluid-solid
interactions: modeling, simulation, bio-mechanical applications, Comptes
Rendus Mécanique, Volume 333, issue 12, december 2005, p.p. 923-933(.pdf,
712 kb).
[21] Céline Grandmont, Bertrand Maury, Nicolas
Meunier, A viscoelastic model with
non-local damping application to the human lungs, Mathematical Modelling and
Numerical Analysis, Vol. 40 No. 1, pp 201-224, 2006 (.pdf,
900 ko).
[20] B. Maury, A time-stepping scheme for inelastic
collisions, Numerische Mathematik, Volume 102, Number 4, pp. 649 -
679, 2006 (.pdf, 1.4 Mo).
[19] B. Maury, N. Meunier, A. Soualah, L. Vial, Outlet
Dissipative conditions for air flow in the bronchial tree, ESAIM
Proceedings, september 2005, vol. 14, 115-123, Eric Cancès &
Jean-Frédéric Gerbeau, Editors (.pdf, 800
kb).
[18] J. Janela, A. Lefebvre, B. Maury, A penalty
method for the simulation of fluid-rigid body interaction, ESAIM
Proceedings, september 2005, vol. 14, 201-212, Eric Cancès &
Jean-Frédéric Gerbeau, Editors (.pdf, 500kb).
(N.B. the associated source code can be downloaded NSpenal.edp).
[17] C. Grandmont, Y. Maday, B. Maury, A
multiscale/multimodel approach of the respiration tree. New trends in
continuum mechanics, 147--157, Theta Ser. Adv. Math., 3, Theta, Bucharest,
2005.
[16] B. Maury, Direct Simulation of Aggregation Phenomena,
Comm. Math. Sci. supplemental issue, No 1, pp. 1-11, 2004 (.pdf,
1.1Mb).
[15] B. Maury, Analyse
Fonctionnelle, exercices et problèmes corrigés (livre), éd. Ellipses,
2004. Description (en français).
[14] S. Bertoluzza, M. Ismail, B. Maury, The FBM Method:
Semi-Discrete Scheme and Some Numerical experiments. Lecture Notes in Comp.
Sc. and Eng., 2004 (.pdf, 530 kb).
[13] B. Maury, Fluid-particle shear flows, ESAIM M2AN., 37, No
4, pp. 699-708, 2003 (.pdf,
1.2Mb).
[12] B. Maury, Version continue de l'algorithme d'Uzawa, C.
R. Acad. Sci. Paris, Série I, 337, pp. 31-36, 2003 (.pdf,
120 kb).
[11] M. Ismail, B. Maury, Méthode de la frontière élargie pour
la simulation d'écoulements fluides, Proc. du 35ème Congrès Nat. d'Ana.
Num., La Grande Motte, pp.1-25, 2003 (.pdf, 1.6
Mb).
[10] G. Carlier, T. Lachand-Robert, B. Maury, A numerical
approach to variational problems subject to convexity constraints, Num.
Math. 88, pp. 299-318, 2001 (.pdf, 560Kb).
[9] B. Maury, A Fat Boundary Method for the Poisson
Equation in a Domain with Holes, J. of Sci. Computing, 16 (2001), no. 3, pp.
319-339 (.pdf, 700kb).
[8] E. Lagarde, B. Auvert, B. Ferry, B. Maury, Concurrent partnerships and
HIV epidemic in five urbancommunities of sub-Saharan Africa, AIDS
2001, vol 15, No X.
[7] G. Carlier, T. Lachand-Robert, B. Maury, H1-projection
into the set of convex functions: a saddle-point formulation, CEMRACS 1999
(Orsay), 277-289, ESAIM Proc., 10, Soc. Math. Appl. Indust., Paris, 1999 (.ps,
1.5 Mb).
[6] B. Maury, Direct Simulations of 2D Fluid-Particle Flows
in Biperiodic Domains, Journal of Computational Physics 156, 325-351, 1999 (.pdf,
3.3 Mb).
[5] Y. Maday, B. Maury, P. Métier, Interaction de fluides potentiels
avec une membrane élastique, CEMRACS 1999 (Orsay), 23-33, ESAIM Proc.,
10, Soc. Math. Appl. Indust., Paris, 1999 (.pdf).
[4] B. Maury, A Many-Body Lubrication Model,
C. R. Acad. Sci. Paris, t. 325, Série I, pp. 1053-1058, 1997 (.pdf,
1.6 Mb).
[3] B. Maury, R. Glowinski, Fluid-Particle Flow: a Symmetric
Formulation, C. R. Acad. Sci. Paris, t. 324, Série I, pp. 1079-1084, 1997.
[2bis] B. Maury, O. Pironneau , Characteristics ALE method for
unsteady free surface flows with surface tension, Z. angew. Math. Mech.,
ICIAM / GAMM 95. Part II, Hamburg , Allemagne, 1996, vol. 76 (4 ref.), pp.
613-614.
[2] B. Maury, Characteristics ALE Method for the 3D
Navier-Stokes Equations with a Free Surface, Int. Journal of Comp. Fluid
Dyn. 6, 175-188 (1996) (.pdf, 1Mb).
[1] K. Boukir, B. Maury, B. Nitrosso, A characteristics-ALE
method for variable domain Navier-Stokes equations. Computational Modelling
of Free and Moving Boundary Problems III, Modelling and Simulation
volume 13, Transactions of the Wessex Institute, 1995.
MUSIQUE
https://www.dropbox.com/sh/ikdfc0ud7wf5slc/AAB_YT8vcyoyVcTJRhwyxl9La?dl=0
Vidéos
Enregistrements divers
Concert du 21 avril
2016 (IHES)
Conf CIRM
 Bertrand Maury
Bertrand Maury
 Bertrand Maury
Bertrand Maury















